偏序集和等价关系
不得不说关于离散数学的定义太抽象,而实在难以理解。
二元关系
对于二元关系我们亦可称之为二元函数,我们一般用于讨论对于两个数学对象的联系。
考虑主要是描述对于同一类元素中存在的一种关系,如几何学中三角形之间的相似。
偏序
考虑偏序其实是一个与全序相对应的二元关系,如 描述子集的包含关系, 描述整数之间的整除关系。全序则相对于偏序的更为广泛,如 描述实数之间的大小关系,全序则对于值域内任意的两个数是均为可比的。
而对于偏序而言,我们可以存在 表示 和 之间存在整除关系, 表示 和 之间存在整除关系,但对 和 而言我们并不存在 ,因此对于元素 和元素 之间并不具备可比性。但是我们存在 且 所以易知 ,据此可知对于偏序和全序皆具有传递性质。
我们定义 为集合 上的一种二元关系, 表示对于有序对 存在此关系的性质的描述,同时我们也易知对于元素 和 元素 两者是可比的,反之若不存在此关系则表示元素 和元素 两者是不可比的。
我们通过一些简单的描述来定义有关偏序和全序的可能存在部分性质:
如果对于 中的所有元素 都存在 ,则 是自反的。
如果对于 中的所有元素 都不存在 ,则 是反自反的。
如果对于 中的所有元素 都存在 和 ,则 是对称的。
如果对于 中的所有满足 的元素 都存在 ,就不存在 ,则 是反对称的。
对于 中的元素 ,只要满足 且 ,就有 ,则 是传递的。
对于偏序,则是一个满足自反性,反对称性且传递性的关系。
而同时对于存在的严格偏序,则是一个满足反自反性,反对称性且传递性的关系。
如 为描述子集关系的偏序,而 为描述真子集关系的严格偏序。
偏序集
对于偏序集的定义,我们认为是存在偏序 的集合 ,且通常记作 。
我们可以通过一些几何方法表示对于偏序集的 的覆盖关系。
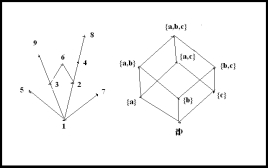
那么,当对于元素 之间存在偏序 即 ,且不存在元素 使得 且 时,我们认为 被 覆盖,或 覆盖 ,且用符号 表示覆盖关系,即 。
而对于在 中存在的元素 ,如果不存在元素 满足 ,那么我们称 为 上的极小元;而如果不存在元素 满足 ,则我们称 为 上的极大元。
显然,对于一个偏序集 中可能存在多个极大元或者多个极小元。
如图所示,对于左图中所示的偏序 即表示整除关系中, 即为极小元,而与之相对的, 均为极大元。同理可知右图中, 为极小元,而 {} 为极大元。
而对于全序集 中,我们存在元素 ,使得 ,那么我们可以将全序集称之为线性有序集。
偏序集线性扩展
现在我们可以考虑如何对于 即一个有限偏序集进行线性扩展,即是否存在线性有序集。
假定我们以 表示对于目前 中所剩下的元素里选出一个极小元 ,并将之删除的步骤。
那么完成 步骤后 中将剩余 个元素。
则对于 即为 的一个线性扩展。
为了深刻理解,我们考虑到以偏序集线性扩展的算法作为举例,即拓扑排序。
拓扑排序的实现是对于图上点的入度维护一个队列,每次操作将入度为 的点删除并将删除后入度也为 的点加入队列,且对于入度变化的点一定是与删除点具有连边的点。
而拓扑排序的实质,即考虑入度来对于所有点判断是否为极小元,并将它们加入队列中。每次删除该极小元后又重新选出新增的极小元加入队列,直到所有点都被删除,就给出了一个符合拓扑序的排列即一个线性扩展。相应地,我们也可以将图上的有向边视为一种独特的偏序。
等价关系
等价关系即集合上满足自反性,对称性和传递性的一种二元关系,通常用符号 表示。
等价关系区别于偏序的不同在于满足对称性或反对称性,通俗的讲即是否满足交换性或相互性。
对于 中的每一个 , 的等价类是 中与 等价的元素组成的集合 {}。
特别地,因为 ,故 的等价类包含 ,从而是非空的。
试证明:在集合 上,不同的等价类将 划分为若干非空的部分,且任意两个部分的交均为空。
等价地,对于任意两个部分的交均为空,可以看做如果存在交,则两个部分即为两个相同的集合。
令 ,并设 是 和 的一个公共元素。那么由于 且 得到 ,则对于任意元素 ,都有 即 ,所以有 。同理可证 ,所以有 。